js根据不同证件进行校验
本文共 1575 字,大约阅读时间需要 5 分钟。
layui下拉
layui.use(['form','element'], function(){ var form = layui.form ,layer = layui.layer ,id_type;//监听下拉当前选择的 form.on('select(idsType)',function (data) { id_type=data.value }) form.on('submit(demo1)', function(data){ let idVal=$("input[name='idNumber']").val(); let reg; if(id_type==0){ console.log('身份证',id_type) reg = /(^\d{15}$)|(^\d{17}(\d|X|x)$)/; if(!reg.test(idVal)){ layer.msg('证件信息错误', {time: 4000, icon:5}); return false; } }else if(id_type==1){ console.log('军官证',id_type) reg = /^[a-zA-Z0-9]{7,21}$/; if(!reg.test(idVal)){ layer.msg('证件信息错误', {time: 4000, icon:5}); return false; } }else if(id_type==2){ console.log('香港特区护照/身份证明',id_type) reg = /^[a-zA-Z0-9]{5,21}$/; if(!reg.test(idVal)){ layer.msg('证件信息错误', {time: 4000, icon:5}); return false; } }else if(id_type==3){ console.log('澳门特区护照/身份证明',id_type) reg = /^[a-zA-Z0-9]{5,21}$/; if(!reg.test(idVal)){ layer.msg('证件信息错误', {time: 4000, icon:5}); return false; } }else if(id_type==4){ console.log('境外永久居住证',id_type) reg = /^[A-Z]{3}\d{6}(?:0[1-9]|1[021])(?:0[1-9]|[21]\d|3[10])\d{2}$/; if(!reg.test(idVal)){ layer.msg('证件信息错误', {time: 4000, icon:5}); return false; } }else if(id_type==5){ console.log('护照',id_type) reg = /^[a-zA-Z0-9]{3,21}$/; if(!reg.test(idVal)){ layer.msg('证件信息错误', {time: 4000, icon:5}); return false; } }}}) 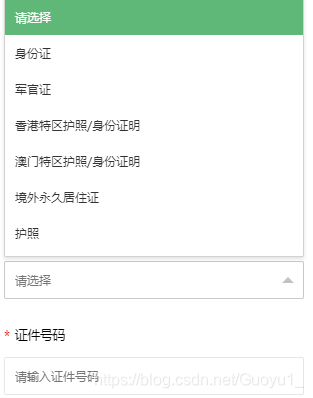
转载地址:http://nwkj.baihongyu.com/
你可能感兴趣的文章
Nginx的Rewrite正则表达式,匹配非某单词
查看>>
Nginx的使用总结(一)
查看>>
Nginx的使用总结(三)
查看>>
Nginx的使用总结(二)
查看>>
Nginx的可视化神器nginx-gui的下载配置和使用
查看>>
Nginx的是什么?干什么用的?
查看>>
Nginx访问控制_登陆权限的控制(http_auth_basic_module)
查看>>
nginx负载均衡和反相代理的配置
查看>>
nginx负载均衡器处理session共享的几种方法(转)
查看>>
nginx负载均衡的5种策略(转载)
查看>>
nginx负载均衡的五种算法
查看>>
nginx转发端口时与导致websocket不生效
查看>>
Nginx运维与实战(二)-Https配置
查看>>
Nginx配置Https证书
查看>>
Nginx配置ssl实现https
查看>>
Nginx配置TCP代理指南
查看>>
Nginx配置——不记录指定文件类型日志
查看>>
nginx配置一、二级域名、多域名对应(api接口、前端网站、后台管理网站)
查看>>
Nginx配置代理解决本地html进行ajax请求接口跨域问题
查看>>
nginx配置全解
查看>>